Mathematics of Circle and Sphere Inversion Fractals

The Apollonian Gasket is probably the best known of the circle inversion fractals. It is described at the Mathworld web site and many other places on the web. It has a fractal dimension of approximately 1.3058 and corresponds to a limit set that is invariant under a Kleinian group (see the section on Kleinian Group Fractals). It is created by iteratively carrying out circle inversions on three mutually tangent circles of the same radius. The image below is an example of the Apollonian Gasket:

The circle inversion algorithm is the following. Consider three circles in the complex plane: circle A with center a and radius ar, circle B with center b and radius br, and circle C with center c and radius cr. Let A be the inversion circle, B the circle to be inverted and C the inversion of B.

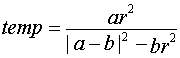
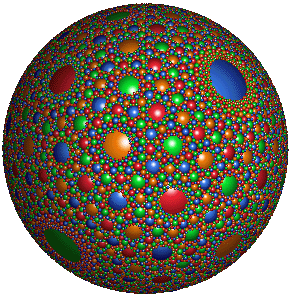
The circle inversion algorithm can be generalized spheres, allowing the generation of 3 dimensional sphere inversion fractals. The image below is the 3D analog of the Apollonian Gasket, which is generated from 4 mutually tangent spheres of the same radius: