Slope Formula Tutorial for UltraFractal - Page 9

Indra's Promise

Kleinian group fractals have been popularized by the book "Indra's Pearls" by David Mumford, Caroline Series and David Wright. The key to fractals of this type is an understanding of Möbius transformations. Möbius transformations form a mathematical group. They are also known as linear fractional transformations, and are represented as:

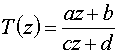
where z is the complex number being transformed, and a, b, c and d are complex constants. A Möbius transformation can be viewed as a composition of translations, scalings and inversion. Properly chosen Möbius transformations can be iterated, with the limit set of the iterated points defining a fractal.

The Indra's Promise ufm is based upon Indra's Pearls, and has extensive non-slope coloring options. This tutorial will concentrate on the slope options. The following image is an example of non-slope coloring using traditional coloring ucls. 

FrescoAtTwilight

The discussion that follows will deal primarily with use of Indra's Promise were the user has checked the "calc as slope" box. If it is checked, the following parameters will be visible. Full use of some parameters requires a thorough knowledge of Indra's Pearls by Mumford, Series and Wright or of Kleinian Group theory. 

• Apply Mapping - This is a Boolean parameter that must be checked if the user wants to apply transforms to the image.
• Oversize by (%) - This is visible only if Apply Mapping is checked. The formula uses an array containing a virtual viewing screen. This parameter increases the size or the virtual viewing screen.
• Max Iters - This is the maximum number of Möbius iterations.
• Smallest Circle -  This is the "bailout" for Möbius inversions. Iteration continues until the circle size is less than the smallest circle.
• Rad multiplier - Alters the radius of all circles by this amount.
• Max circle size - The largest circle to be displayed.
• Min display level - The minimum iteration level to display. If Min display level equals Max Iters, this will display an approximation of the limit set.
• Group - The Kleinian group to be calculated
  • Double Cusp - Calculated a Kleinian double cusp group. The particular double cusp to be calculated is listed below:
    • 0/1
    • 1/15
    • 1/10
    • 2/19
    • 1/9
    • 7/43
    • 3/10
    • 2/5
    • 1/2
    • 21/34
    • 1/1
  • Grandma's Special - This parameter utilizes a special formula developed in the book Indra's Pearls, and requires a thorough knowledge of the use of trace parameters. The use of the explore mode in UltraFractal is not recommended.
  • Grandma's Special #2 - This parameter utilizes a special formula developed in the book Indra's Pearls, and requires a thorough knowledge of the use of trace parameters. The use of the explore mode in UltraFractal is not recommended.
  • Masket - This parameter utilizes a special formula developed in the book Indra's Pearls, and requires a thorough knowledge of the use of trace parameters. The use of the explore mode in UltraFractal is not recommended.
  • Nearby Group - This is a Kleinian group near the 1/10 cusp, but is not a cusp itself.
  • Schottky - The user can chose from several options
    • Kissing - All the base circles are tangent. The explore mode can be used on the numeric Kissing parameters.
    • Disjoint - None of the base parameters touch.
    • Apollonian 1 - This is a mapping of the standard Apollonian Gasket. All circles are centered on the limit set. This option is very slow unless Max Iters is decreased to a small value.
    • Apollonian 2 - This is a Masket type mapping of the standard Apollonian Gasket. All circles are centered on the limit set. This option is very slow unless Max Iters is decreased to a small value. This option is very slow unless Max Iters is decreased to a small value.
    • Apollonian 3 - This is the standard Apollonian Gasket, except all circles are centered on the limit set. 
    • Indra's Net - This option can be used to create the Indra's Net image in Indra's Pearls.
  • Slice - This is a special formula developed by the author. The groups are a mapping of the double cusps. The particular double cusp to be calculated is listed below:
    • 0/1
    • 1/15
    • 1/10
    • 2/19
    • 1/9
    • 7/43
    • 3/10
    • 2/5
    • 1/2
    • 21/34
    • 1/1
• Cusp View - This parameter is visible for some group selections. For Grandma's Special, Grandma's Special #2 and Masket groups use only the Standard option unless you have a thorough knowledge of Kleinien groups.
• Height Transfer - Slopes are calculated on the "stacked" orbits to determine the lighting effects. Height transfer applies a function to the height before the slope is calculated. It is useful for special effects.
• Height Pre-Scale - This is the ratio between height and distance. Larger values will exaggerate the lighting of highs and lows in the texture. This needs to be adjusted for most formulas.
• Height Post-Scale - This is similar to Height Pre-Scale but is applied after the transfer function. It is useful for special effect
• Fill Type -  This determines the lighting shape for the iterated circles.
  • Quartic1 - This is the ellipsoid lighting:

    (radiuspower - alpha*xpower - beta*ypower)1/power/gamma

  • Quartic2 - Hyperboloid lighting #1:

    (radiuspower + alpha*xpower - beta*ypower)1/power/gamma

  • Quartic3 - Hyperboloid lighting #2:

    (radiuspower + alpha*xpower + beta*ypower)1/power/gamma

  • Quartic4 - Hyperboloid lighting #3:

    (radiuspower - alpha*xpower + beta*ypower)1/power/gamma

  • Power - The power in the Quartic formulas.
  • alpha - See the Quartic formulas.
  • beta - See the Quartic formulas.
  • gamma - See the Quartic formulas.
  • global fBm weight - The two global fBm parameters are unique in that they perturb the structure of the gasket shapes and not the coloring of the shapes. They put texture on the shape surface so that light reflecting off the surface shows the texture. This parameter determines the intensity of the texture.
  • global fBm scale - Determines the scale of the texture.

  The first image is the the full 1/15 Kleinian double cusp. Its fractal nature is clearly visible. 3D Texturizer Enhanced III is used for coloring. Generally, Direct Color Slope will not give satisfactory results with this ucl. The background was done with the non-slope coloring mode of Indra's Promise. Examine the upr to see how the image was created and the gradients were used.

  1/15 Cusp

Cusp1_15 {
::P4Msxhn2tr1SvNSuR47Dw8fQQnSymxufq2OB9BxZ3DG7kggsbAyNBqupk64+lbSZLLs/4T9g
kd3SeyiFL2AEE7TFfVVxPWV9xmy7GkFGZ9f6jfYxCTlpWlv8zH19hbCTXu4lqSzh8VJBLOoq
2fwQi1yXVD68YcF7lNNy8wbyyCm9X0iiBVZlRnv8v31KrLXIkDtKj5PHeb093GFEkt8jfg0E
Z5Gl5QXZezxaTVvUrXUI7NVdt5L/COnFhLX01LLqMvmHGEswMIb19yBVrJ/Vl+jfoR23X1un
0VB0raIP42gFNy9to3l+xPsrbA0uktm8UFOFUV9qhiDqiHz72tbxuqaVrsBwgB12bOurZ5CQ
ZDvmv8h2yBp+vN01UpVLRl0v5ZAGQfMGVzGddXvC9GQG8m6X/LsPZ7CtDorHaLyDuJgVQt6Z
VN7Fb0FVDFA6DDGEEidoq3KrqzX+P0qFoU3RzSofrYUeCrEb7cUJ1WccdZJ2qqti7vv7Fc7C
IyuN7arazrKBfhX/gsEAGAlwJCID0GciVs7pP09CphnlDVSAtJXmXls8fNuVKgYGzrAAs8b7
OutWtADiWaHAscYKtHxGL/rK5w2XXsfo7YvFKR7QDuuGOYalG1kOby/BjstUOgbK9xtkd++K
tGQXe591HhItfoRWXDBLDddESpPC7qwkYU8EIef6doDVNgudILqx4EPQotwAgcKdebHPHJFL
x7Z7EQxGQNp2JLhJzaphUeYU2dprCWFGmtKN+Wy2p3HGEDDFmdPMPjk8obhZHhN3mH7cEZtx
I3ymHEWLy/UE5AUYP3/pdwBKZ5Bo1ZdhkidsxEc7I0ViQXEirhApnOKHMVFYyEAZvMkHRGr/
A4KYgkC9JWB28aUqFSM0KjFD2vbbzOQv8QWzS9PoeiXAlal9xPU1qhwMuwC64oH321q+4Hgw
V/QQgoGTrBo0PL7+S3VXBxiXmVWUTBN2Ez4vdzPqOZOOUdWNs57aPIbLUlbe4hHWyIWvFIBJ
9xG/5UFNEAQ3ynokx2aTWb74sZOCorubATk/n406HUQCSoPFmD6fodHmspWUjlJRLLb3DQTY
UApdFk3IpCarGz+77qaNYgZqv1r0ZSdftsVlzBXg+OxJ3o4r5uVjtOTDIb2WhVCZTZI0Ql/F
pBOsx8o9DVlnsBuo8rjuP0PvKoT7ytV65p/C3gHCSrbxaDp8aN2ADL+1AZdH8Y9sDSIAcLmX
ExS7G1x8gLX8E7I8QP8Qe0tUGyMfBYWSdbCTReG1JGTH+dfCzy7bq4tGWwLOHKVQSh56nGIp
ocZRHwcsHSlR0jpO6aaAZsWSVTPUFDG9VypW4m3NLXY3qYoyQnhPW/UMxHW1WqAoONbBF1AS
pZBRZrcDsyPwqsssIoqodgsM2+vxiAVbHA2vWWQybHhceiBeOyo00fJsrRvzu+/HsrT5Rfnc
9dy18ooVJ3HlEu6dW23ZZ/fWW247jzSh68/SIZnvmfL5YFyiHxqxtlzoZ/PTrGF8fNSVKY6X
Jn6UKVsM0Mm0p0oW1YRL75/PPZ6ITaslJgpSDv5uvCVa4Ea03JRfnE9XPJa2VcoXTZ6y9WbM
47q1N8jIh4FJfwVmRyqTQCmZk2cTTXpK/z1dal24IE5OfA8XqAolOpSXMoMYm7AEQtgWKX96
Orygsg8S1OJUNiHG24cNaueMqG+x9YgqknCmEbss52kYoMDXOA7uFo2DdhA1EMyDqfsqnQ52
uNd72gjop2o0eJPWPwVqGad5joCXbpbWbbLstF22NwqB4tpq93t+PK+9EQubTzujtFrtVGsN
F5SIFk2sQ+7fY5UFI3q9R/A4ZYtye+uNWjwHEQi7aoskaAKECbKK5BiJpuh7kUbLl0sOf1NR
3FHenVlUcWheNGQT5wNgck9S/wZpmQC6QEGI0VS6Q468PRFeKOEBixkU8a6sYUvHW7LIcAXe
qvII0RV/MdjKDVLkqhSRsuQdGMiAkaP0TqF/YEWrWVeor/CvFG4JQlx2k3nsK9pY2ceN+UJp
RsvnuwPhU7yZaF9uaJt/JJQnR3cPJi+KXYXmgiZX441SrTVL1eDiGpWamZD6Ao/xz+9e/jvs
2Wno/xQ0iRJkcEBYxkMY+PBfjWK1AcgPFBj4Wf6aKVq/RMoD0AfnHuJoE4k23Me+oJ0ocEM3
TKPhJ7s+HZEt/RajFa3X9P+mhP1Vh8BRdVkT4yYn6K3IWoa8I5LQk91wlZAPTSTJxI7xjZgP
Tu4gwMsm/k6YaOY0nLk3McdMEeOcTc6lHnnZP8M6B2Vfuy0d96Pow9r7WtjxxKbUvSv2ePfK
MWBFxuK1Q3jH7WK9eLsp7ptHPeiT0bAdvbaoBGBQNUn4av0vs9E4g163P5QDX4e4eBv1S1Ph
pkWh28ZaT/0ofjJXxOnoHues569ZcpVVgQrTaMTAa4TFGtBuoQ7c1usQyKxzzeT9aBIo8GCl
bn0480RYzdxZnTBh+p5wCrVheu2wIVWyIBwu201+7JCfS4a7nvofkMKLbgy4Ujb93mlv3gvT
i84ZwZIqAUU2AjGyXtqzsWbU9e8D1N3hX7cT3Fh6n1GYQE5fGKW7SdZWFBxqQEGi3mSRMhSR
QfXwi3kVRwwGQpIGpUEeKFhLwdCriYCriYs+/FUKCLliY82boiZWFx8g0D9iRKFxMCg5sKCH
riAYVIKFhlSRkfZ+9TliRWlJ+5FUKCHlCu/tosEUrnVRMyqgiZzpUEeKFxF1JnzqI8sKsHDU
KiRKFxEKFCw8EHg5nwqIYWFmSRMlSRMnSRcJpR88JkImx5kKumSxjoAri4rxq42+VhCHliT4
NidqrcDqFTJgvgSR4pUEIli7efYYplVxdmMhSRMjSBc+Jh8mhrd5zCmVZGliwSpIc1MfDWFh
nVRYpNmQpIcUKiRGn3iVR4YVEE5FQpIcUKiRKFx4jxMhVxNTNL8GUKCPtxIriYkVRMWq8KKF
hnSR4rZByXxqY9bMz6rSpImUvX4KpLGZVEu63+UhpF4H3EIri4ryqIcEXQNfxEiDR7ESLkVZ
6gvpFJFMhSRMj99KWF0wEliYKliYKliY8NQwK/ipsKiJEIMli4CKFx4HfzsKiRWFxIJCq45U
KCHFy4nMJmwqM/x6+KvHYwP7jASfxc4sHEESQvlzRHth1H052nb1UgvOo7FBJJZZJaU+bpQp
Q7jDSPJoj6mfVQScVO9yY23SxtyDyI7bbcAwel/OX0XDv8838Tn/J8D8OzDHmv02BNhornRE
PjJaJ+6JF7VD8p5h2DIQMeUMCFZtAtSGHIdUclV08ij6/lIvU8kzyXS8dn6lWZlgPi9bAAq9
IWU3HVyNjG/BmcdFfxUSuoda+Z1Qnv5Kqp9D5Lf24+E/TQop919guL5zgSVB2dALuhepuz2X
xBuCDgt4jcs48S6A1cKZSSk5UqPLCXM9wYfWVV7CFgOpPc/AZ+KpHqOVtNyhknqKcyoS4QXH
lkrjI+7eUFmTGnIwP1AebEdyILHPwklpjHlkKqOr8rSvv19TNW+c/eGG23KHq34QCu1lYR8l
YxqZYRmHLwta8kta8o3g724JO6qJyZWZ26EYSXfEV/+c5W7L7wDjoC+auIczzA72j2jTyjlT
6Ky+0aYH47QnTi+uYcdcKM8NVLdFG5zKNVSHDxGcv0Fe8wlrY0zCdpeozFaYOFGMD+CDHxvB
AA9X1GAQXoCIXMNJVWCKZEADnkXb/dY1FF58lRwkesaI9Oh+Ku9R27KCixWR9BQVMBDIF5li
9SJMagO+5hJ7izVTaEaOhlF5GRQjxhihWS4mcWIV1Zh8AbLMEF5U+t4HWJw+ThkcfS0qM3PR
CcNd7vqSQIcbr4I3vqSw9T+VVyCSTuL4qfhGo7wkk7t9j/kMc/p3nFEnNa6o7cGPOJNK+evx
9WPNdVaQqz4xrCn8/NRSYyq0kwfR/CO/bMdtSlD=
}

One of the best known images from the book Indra's Pearls is called Indra's Net, and is a depiction of the net cast by the Buddhist god Indra. The user should study the upr to see how the image is created. The top layer uses non-slope coloring.

Indra's Net

IndrasNet {
::xTEv9jn2tbVTPutNQ07Gw/HE0leaXrPsssbBPkFJHMQaQR3UgezgmiSmdpI1SSvr1+rvzQSp
ddAaTCQvUg4Le4QyhvZ4beitGKzRl/8yFJJOhTyJp7VNGq9TcXayziG3Jy6sskTcR3Jn3USH
5GLpA3SHtvnSyvtuO7qfFJMDvR4sk0fXroymk7oGF35+l8VlZrKyyqTXuwHJ/R3zdn0Nk+zS
nYgatJM6gToVk0PirJJPNRPQZC3IJHgQP30x71Nci+JuBCzyF90hBhqzHNGX54GyNZ3mltJ8
ra1bHk0T7UAs3Umtuc92EqqDy88tZLX0qNAKoBURvIwAhH5A3wOxZPQ0ttJtCJXR7hilhf82
zt9pJwRaGnKe/mR3Ls8UMIDHAIaxcpADzBrUPwJKNYCQWO+rBgH8gnCEp9KGBwbY7S+TcJpC
3KTYYAQxUJHHzlHpCJsVFHGi26zuCy6XHQmCSsCfvofQiLWKUCYW8M1Pj54qsk2DtKhiIaAI
ATYoNQpAKTxYAlDwFpIgJ7J9z+9/E1IoKHhpPPtNazf9K+ZntDuRInvndS7cPMG9BHZeIrwB
pfiTNHHT6M6zDxCHeE+JvT7O9mx9k7dUVD10gOPf0H9Qp/nsJIzNs/B5ZgAefPVKBOkRrBKN
uBIlyXXimXAzdVbREJMIkzDmWS2qI8h0xi1gQNjbDXUwao4ai5bcBoZPEmq4ipwij1OfwzLq
3WtJbTee9mqyV+zuaXeWJMVe9OYdOqHRIbFrzujkyJgQlOH9Y44Bj3dH5mCPAcGqKCrLtwVp
/kNwoXsMqnusOEhw4CEKFIEBaskk+4ZqxJYYPGUye24vgpyhTAUQiEHxUIAx2d0SB9BWuLWD
6aP23CxNMV8Y9+N8HDbw3JVvchQZBCWQwBBOiYkAvcBQXnnCogWsbvC6ZmXWMx+iuPmcu7DG
fjtHunPxvMTi0SRTssx0SNKd5vsGoSIwdcSR1GvDmW9EKsQevw/vytcRHclKALPoChGDlQ1w
vAZoPgk66dVl7iOLK3GdDX2l5Fbj+Lz83jhpyrKyWvuAKrRZt/h4PJ6VUV9tJXeHl9A2Cpau
Sx8/d6jjc73pAZ5/iAZ6fY5JRFx0rUKDRYWs8NKlvrp5bQmcWjIqU+1lJ9o9Hyk/Qm8/SZSo
U+1VJxNEbDLf/hPzv4ObEvwNH+g6EVx4NH2vffaoSNELggl9c/89jwPFUYWFuJjirhuVl+Nv
txrzhtt/JusBDHaJmfJhciK2itX8EJ+4S8kjCNFYs5QnC1rqtzzqG0ClDZiVxg4dMGa0GkUF
nEIUQsuEalRzxXNfZ61Q0+jooOmIYS6rEcyHpO4CGfcUnR0cJSWR7xoN4cufFcG3e8txhl8c
YQYqjwVQTko7iMh5iwrq9Ru5VkSgpAbsIY1GjxbYThYMxhCAJM7+9kiV+uirwC8W8qgBjUPh
BkHn/hbwO7hehP78yblErQ5tyJ2HNerCClptfxnEZ6+ewG1PCvsEmd0Dqkp1db60H2QaiR7C
XqFbx9H/m50nMzmcM7JfTdddRe131XK/bkODk4N=
}

The Min display level parameter can create some interesting effects. When it equals Max iter you will get an approximation to the limit set, the set of circles that is the convergence of all the earlier circles. For small values of Max iter the image can have artistic interest. Indra's Necklace is such an image:

Indra's Necklace

IndrasNecklace {
::kvtaejn29aVTPutNQ07Gw/HE0l2eI2iSWW2tgHyikCY0mggutA9mBtElN7SRqlkeX78rvzwh
2r30W00L1nGNkc+4NvZG37EtBh+7nOJLLoCaJPfjpzJ8fU2+gW0KzzeW1FOwXuoI7gUt/QgX
zKz0izSnnXivbvYYQwZzaaKe1vysWnsTF888fxaE6us7EOjME+B28qi5lFFN5TnEtU0/DywB
bHf4oOoGFefWrYMosGe+di2H27sHNd5Z2RRrKcmzKKyCOhxPKcSTgfW6nOZQMOqM7jmrF0Kd
8i5FZDi9GMArnOp36AHIIHKOpwrgmaU6aPA5M323n1r0SjYAADnc3sj9D5ZgxcnvAOfyZHUe
ZOakxtPBIBGmVMwMb9a7oEjGQGiG95PQxUSF6HwWbMt8iZFkB0ynkaeF+4WlrFKCwRFM8bpe
nQp55/mXmhS2jhcQfSskvgsQ6bOGA6EO+2uO8LlRR6HtPj5KAH9b7NKDX1BBC9enoDQFAiwL
CwC8NvkiM/B7zxY7JhTJAgOGt0bEd/xLZR7R/Y4Mk733ewGCPcOpDcJrOmb4H5fUKc7Onhlz
xEAiuIe49BhpT46uR3wrUecX0D/ky7BIle9o+IwwufQo1SXmzajIk/IkNsFRQ9EW7x0BQXMe
ZkoH5GXzffK7BAT65GLdHRk/QJb6Co4AYm60lFwlJrMENOrsZV9yilMWzy6q5sZrrXVvmVUB
HxaWD3Lgmad9c42YUF2xruEICdII2RuHEe7d83UGDgIVn0fqHqjtWkN9ZfrISXY107JFlYg0
gBIwkB2zjHFugqNrCRmxndxarQPeACEk9IxIiMQqZGlMQrgXGSIw++dD9oniHl8bUvT+I9gY
zUz0JKjH4W0MFMsx41YNypTAO61jA2nHbknVW/y1iAqLzb1qOw8fRjYrOyYS9iVvb7vKPFO6
UfW62+ezBhpV2tdzmN5EgNmwRQyfc4aZSFPCQo5UBN6sdp+TjlagJCgVbdYv7vjXb0Jh2C21
u2IVEmI0jtYyMNOcE9swsHwGWFi/SobREHitsgoXjWlJgMyUFjUcma3G1CjkTMLwanoGaU88
LifmfhsMsThj+ILHiYhk/ziAUrlYBxp6OlYto85kMo8aXLoM9800d6KPTfQHtDKCdJGfIRKu
CD+Boj7wVk+VlRg/tDbKKJp+kNuhYR2IRnY34gNb4lzjdHvKUglJ1kQLv5SIgMa27fzKUcQF
Tu4MuKOMlIKx4+HdRpSuAadmOZP0GjgHtqwOMAy4YE1woWCTnEnjxU2l7NLPLlpIPxZDUV9N
M2S0CKTn8EvZRWkywZLWsqY1q6k+VX1vspppkdR/6Fk3/beCa40JQWmW6FD2XAc6mFXXJWWX
//5+0/hlpftrSHVnk6tU1OtI4CvYWRFbBreNOhc5aQ+reoy/+gEvYIOI5lpI3/j39h4gRG0k
OfZqvcw2B3+TSHYpvxjnbi5XZckRwdzKdcxKjPjWyBkmOl/m+DY6EdW6fhgkag/wLXN7m1y0
kIYr89AlN+3Egm5dUVIaGpEm9UWVseRcHkpjCw3peSh/7jMaqHok+zCAfP8tqvLBsyRPfG+f
yYYTAjLPN+FtA/VWFR+qXVtidlwyglKJ6adz6iqyk+K26bYylFAPn18fi2+n00jZBD==
}