

Mathematics of Kleinian Group Fractals
Kleinian group fractals have been popularized by the book "Indra's Pearls" by David Mumford, Caroline Series and David Wright. The key to fractals of this type is an understanding of Möbius transformations. Möbius transformations form a mathematical group. They are also known as linear fractional transformations, and are represented as:
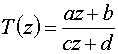
where z is the complex number being transformed, and a, b, c and d are complex constants. A Möbius transformation can be viewed as a composition of translations, scalings and inversion. Properly chosen Möbius transformations can be iterated, with the limit set of the iterated points defining a fractal. The fractals created from the iteration of Möbius transformations can be as beautiful and varied as fractals created by other better known methods.
Möbius transformations can be represented in a matrix form:
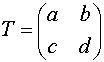
Iteration of the transformation is accomplished by matrix multiplication and inversion by matrix inversion. The matrix should be normalized, which means that ad-bc = 1. The conjugate of a transformation (conjugated with another transformation) is defined as:
![]()
The trace of a transformation is defined as:
![]()
The trace of a transformation is unchanged by conjugation. Möbius transformations can be classified by the value of the trace and the number of fixed points (one or two).
Loxodromic. These have one source Fix-T
and one sink Fix+T.
On
iteration, points spiral out from the source and into the sink. TrT
is not between –2 and 2, and they are conjugate to T(z)
= kz, |k|>1.
Hyperbolic. Points move not in spirals but in
circles through Fix-T,
Fix+T.
TrT
is real and not between –2 and 2, and they are conjugate to T(z)
= kz, k real,
k>0.
Elliptic. Have two
neutral fixed points and move around circles round the fixed points. TrT
is real and strictly between –2 and 2, and they are conjugate to T(z)
= kz, |k| = 1
.
Parabolic. Have one fixed point that is both the source and sink. TrT=+2 , and they are conjugate to the translations T(z) = kz+a , k = 1.
The trace of the transformation determines if, and what
type of fractal, is generated upon iteration.
Two examples of Kleinian group fractals are shown below:

Indra's Net (A Schottky group)

Kleinian 1/15 Cusp