

Attractor Traps Tutorial for UltraFractal - Page 5
Expert Mode Part I
When the expert mode box is checked a number of new parameters and parameter sections become visible. These include
Two examples (and a base image) will be provided on this page for the first three parameter types. The remainder will be covered on subsequent pages.
The first three images, including the base, are for Limited iterations. The Latoocarfian attractor often gives many distracting lines and busy detail that detract from an image.
 |
 |
| Base | Initial iterations = 10 |
 |
|
| Initial
iterations = 10 Iterations to trap = 2 Iterations to skip = 4 Pattern repeat = 3 |
|
AttrLimIterBase {
; Copyright © 2007 by Ronald Barnett.
::Pjb+ujn2tv1SvNOyR47Gw/HI0pksxykNJFlTQfQ9GsA7iJPQmc3oNVLpGmvMZ7xyC7P+UV1P
IlkHs7mgJIH4Afo6XVVsqq7vu/G7d9ySjs6Pd7NRRGtpSxXsxY6/ku+HNqehcQtI6N9WzB+q
s4oDK9+DGeeCLqS+uqfgnhLcvsuWyTWWUEf2/YRl9qtazAfx/stRWtNSI7bUGzfO9eG8Tccx
ibvh0E5A1Kzh2t86XrM6O5wQUpszobb4L+EOnI2io2OZp28OPJOOy0LbG6k9qGD/d1gVD97V
1tbV8h2dmK0bv9maZXnuZPZiSYyqee8ysk0s0sHKyzuPeZeacRcaxDsHSyjql7b4JFLjXlnk
mEJb2DRl7KYLzjXVc7N7a7BHUadY5RNqOwbij6U9lHUlPzb3tLanuS1IrhwZv6plvureREY5
+35L+pXr0ShUX1+qZBqkuHNqBDH8aQ8J7AkGBV+YXC4rM2q8Vscon1kzmmweY9awZv9Gdzge
rym+wwxOwbaabU3eDolrHqS3ok9R9qOl0ATMaotSvlnl8QWac2ledZF5gOHHrLgil2+/Vvsb
YB4cfBqAw0Dk5hWqjQEgyE4nEMnHpExPo7HM2vzy2q2ebvY1lEztQ3b1DQdiBsqXKimJZDY2
UDblmVxfR2z3q2Jh6E7M4JR7ecXTKXW2iW3WxChKU7042FPowvhOKCRBbIbN6vNvWDKq7RZV
FlVtjM8sujHbXfT7jt7eEHcgjZHUaPoPKTJNQrGSG12m3sbW2M63CXXCXbqalvoW38728HF/
+FwHR9uXbK3whEXjx3UwlGZjVN1td8F/hFTVg8pBMTSxRjVlWPf3jOL0068h37Ub4fSaabLl
970SM6DVj92B6VyKMLVvhvaJbdaya7yQ9OUKrUlDbgga8aaSgMD/Wh9AQidgiFUGFGIBHo8Q
yG+dJ5uc/BG0KlkS3Qx5R9eg0bCNIuc3aIVfQ3dmuxcKqZYLMKxs6C1Z8Fu7hOStrwhJt6U5
h2ur92XAVm6qxexp0XStmLoxX2SaE77lL8zXeVu9MtieXlkCBkEoT2yHIR0XXumEzQxiLc8K
pzpqkDBDiGpSaOzGUCo75Thv9unfDkv32dCaRWGJzoAWKJDm/u4lrypGgDcHDGxv+8N0mpun
xKPQDD6mQTQJ4+Lfz0zHNjGF1jvnc7Em8l19sNi29M9hl4+u6e+iEi1bq0J2ERlm5Fus2pS7
HxFqGTJfCqsvOcZ6xcSeOJycpHTvNncRiw0T6MOOlmDW95L5N9XXDh5hlp5XmOPZ9wToH4W9
Jtp961fQhfvLzvsOW5q6VD0w+yYFcM2VbNG6w0u74uOXYboj+8sjn5FDGYozPN0AjBwBt6D+
KDLbPFcwj+3PJphLcPA3+RLd4FcLpTweU5oT8yofjbuS9ORXfrxc93Z6WnqAhGv04OBoRYrw
oNwFl4m7gfXIZl0z39mH0CgWFMEK3MpxppjYN3F5OvCSCTzHLcWF65aDjgZZjoA7ay9NA0pG
bcngmIjalNwx4UD4KCOvAuICg4F6kgP+C4MEaBKKrhRToYEEk3MYUBoOS32OCa328+AC302A
Cig/9wh1+tuWUFxIqiwjqcOkiYCkiA2iO5o/zQVEBUFBiqYhUEBIFhvwdCqiYCqiY88/LgUE
OIFc2OAAUxWUFx5FpH6EjQKizAAOHVR4RVEAqCBpIcQKC+l7vfZrYEVZifeBkiwDpgf/uosE
UbAVRMiqgiFnDpICQKiLOn8cUFRAVx6xAkiYESRMBShCYBgDw8TQVEWUFLkiYKki4cIFxlgG
pnPhMxZYO5irhUCRUAVR81QV8f+6EhHSxL8B1OVa/gDipAwXApICQKCESxfTPss0hq4zJTgU
EnBpAO/kSeT/1u8JhFV5MIFhDSR4Pz8DQVEBUFhD2YCkiwDpIGRc+IUFhHVRQgXAkiwDpIGh
UIxLP6rzPzBrwHApICwGjoKiRUFx4RlXBpICQKiwZWg8VoKO/G3Z9VhUETOvX4PSXMiqI8nf
H2KM9A+xPCEVR8VRVEegL4MfxEgD0QThbONdwP0ikCmApIOD99KUF0wEkiYKkiYKkCF0HP5X
MFVRMBAxCpIuASREeihDVRMiqIGBRQFfOkiwDhM5RSTQVcvXyaoLfEL8AnnqHd7Grr5WZDFq
crEm3OICZ1iba3lcvdP6oNc+wAsp2O1SeOJ09G8EfSSudLaUCA1gSY3Y0MhP8SvH6mZfHKKu
i33+aD+y+hDtv5X5BJzKVeAi9qwduonGv4039zn+Z8JensDnwX46gmA76ZwszYiWSveSpB1A
vUPxlgAx0RRGKa1C0Kbcg8RxVORzbeo/3YBp0J5y3yCdnHkW5kgnx+dQAq5V8Q9QVptJz22G
NtdlexUyuodO/kqvN0cF106HytfJQKxRo0koOi6er7ZzqSs7Yr4j6Gthfyu2TwVYgYLS4R0p
FUC1cMbymIzx8wuIcx4Ve4fvSX5LFgOpXvfgMvWGCVH1Px8Ryj6SvMqEbprHSy3Bz+uHVp5o
xLC4T1g3yoMjc7YCTuNfMVSqQfSFW1w+GXEBiCd7thh9Ny+qH9RCbrLjFpXGLWdWsoIELwP1
0JfqpjeD+1mOxRXNRuwJbtOFMprPiqfPX+0gVF2hxoCAKQhb7MwuDR7xJFilT6yGNtdgM6xJ
xQX2464Ushvpapt0I/iagOSHLx6dbt7x0j94Kb0zF6yDhOfph5YS8Zhvkkx4XPEADX1GCg+S
FQuc6mU5WQJjBwkJ7rhj0w7pOUWytXGB30jnG2reJgXA9yc3VEETdiDHAVZBYAJWQKNIlZjG
ojfqfyXxJ9kGJmj4xi2GMox4QpQLJcTOXIV16C5xuWYJKipsvXuVDLySebbdNIPwX8ZddXlK
CG9dKdG5n3yFRD1ttmDUBOA/QIg8kCyd1w+xjgNsMKyYFpMXf4hC2eXxyzXDX4z2PL0/6044
s1sR1kGGqoIed+qV3ejjdayZduBUV4tqn7aGeTxf9sen8bg17ty+nVNzUeHFBVaDUw+/DJ/2
eSAG01mX3qWMlD8GIWTPYOQ896ZivnJ+em47ZivnJ+em47ZivnJ+em47ZivnJ+em47ZivnJ+
em47ZivnJ+em47ZivnJ++DJ+ONdkxaohjx6YPH2heSWVUUww71/NhE70fBSsnJs+XimaWReS
2q0M2/LZq+vA39S2UqmZoemh6ZGqnZoemh6ZGqnZoemh6ZGqnZoemh6ZGqnZoemh6ZGqnZoe
mh6ZGqnZoemh6/b/VzGacJD1he+mxQtQW+8eCL4MSq/YSphUol85vCLz/apYuTfUV5wsXM9N
hIcXaSWS+DIK+qHA5i/T5Q29L4MbNLddG8zE/ZQWTMH79nP/Di/6P+jL8A26BF/fo6roL0TN
74LZ3TXqcXC/z4Wo9395Dy+OsHLoldx7Y8/evGuUI94ydd+zPJE0/mn84nUGpD5ur9NwlZeU
eqJzPGefD6tOd2DwhbmoGs0j2BDmQDSnBs0dIAUZxZrtXAiuwiVT7qr5ZWdpxUZH/Tt7l9az
hadJi3XOeRjynqcrq0U5upS5T9eJjXS1NQvYY132/QFgah1FJryv6/GnkscWWcSq/PWB8vBh
I/fUCsk0kkifT7W+3Qzdi1D=
}
The next two examples and base image are for use of the Progressive parameters. Progressive parameters increment the base parameter with each iteration.
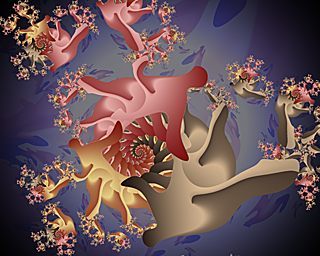 |
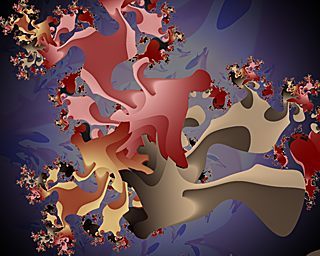 |
| Base | Inc skew = 2.0 |
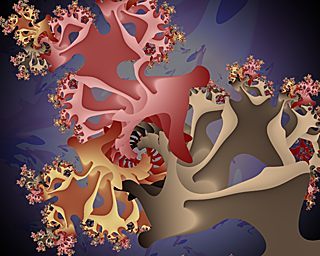 |
|
| Inc Trap offset = (-0.0038462,-0.0079882) | |
AttrProgressiveBase {
; Copyright © 2007 by Ronald Barnett.
::y4oojhn2tz1SPOOuR47Dw8fwwnSymxjea7OB8QzBIBBYXkgkcvBbJabFrXtI7XG7P+UVRSJK
5uTmJb2gFIcwcoKSqiFrqI/k+oRfYQUoF1/uP+hVr0V6aJb9ta9wfZo74gUpqeSyFK56VPXV
qPx2mFt6ks64JNLPOZVt4V5giljP8RRTjgFvZ3uoZ/LZVxgssSrYr/rdti6yVcxQrUr/9pfO
B+fU0u1f8DklInoRqP1VyaesWX1LUqVFiedVXLb93jjZVy6Vd9iiK9rs4ooV6BRrqXMIb1sX
lKjFGOKb6KlMV3BdN6tf8DNi++q2j0UUADWOw+U0msk09Jp7ySjz/MoFnmFFlGlsP9m8VNij
tsUY9cT22byWJaPCBnoNJxpxf8DH6GAPUY8YxLVo9A3JaVvco4ks4Mr7whVHqqltiGImOIvf
zjHaWvCm6hXZr/jwaoWJaeNdNai+70SlmBONIevoqu7RNZPwg31HDTb+OyD3mAB7qWVVp0ky
wl/BYyb7alf8DwjddX1VtSxwKVXdVJLL+ms0osluWRN5HWvDrAgyiuh/+goXtG8hng8MmEg8
LoJfBWmU8G9cYM3Rh7/Q1gSbWOFd1dDmW/TQsRgZQo5yKFUNohZ1JtiGJNHwoJFWqNkAG+Jx
ArUeQAVDmRwiXd4uDtpMRRHO7m6yoNbRrT9beYlEXD9UchipQKZyfbfsBMU/di6aK1Z6Rduq
nFZe+2u76OcH2pihJBU6IYPKhI0gWLJjW72nNbJudyv52m4Wdqmktupq9Xd7vl/rXDLimDP2
WcLDSXtanKnJ0iWjZa66Zr/Nr9Ng4eFsgMxRtxkGP/wd2Zotz6Dv2Lvl9lO1PIG0VYovuCko
WHkiaMF1cLb7GoWPev1iqCRtsQdLEOj2bzjNgaCuQhqcIrqoABlOhOixOKOFfL7Tx5kYCImS
Sp36SFTm+EZ6Yqf8xzd29UV/MDjdgmFq4N2ANM+coZj8t5peymY63YSbwDs6pu+r92HArmmh
CWL+AYx8FO6DlkRRv4Bf/8hHFlzMJaoaBt+NmoWAmNZzNkI6rb2TiZo4O/5oWY9oahJi7551
C9sphSA9nvYW79nfGE+sRMGnukMSOhCY2dP9nhpHOibbOpAOwnSgOJl8bptR9nxaOwCKoCxp
CGBSzoNctkOfAZ0AGVzN96ty6PPGR7PTrtY76q/81Jk6qYTiouKxJ8G1O1VuOVj5G0kfPUWf
dsSPg5k8c3GSssMmkGzJjWWPQGEO4nGAW9FNlK0DX7yYeYTa+s05Fj7dB9gpn+Slu76n/kEX
ybynVHLtV9SF1nXZsEOD7qdHqeMzTC2wmqnWbmOp6tll1qe3IVGB08qK5yl4iH7IFfwV7R3K
AfwjAcq8NiOqHwtk2ThB525bYVPY9bcnVqzJ6H60zr5tOvKt0U1jCtOpLjtNuVYaCwnwtIAF
lLjTTUa51hy0SAna0iocLb65B9L+d+mzIZg4xx4FGtzK04iJGhxymO//QbuTBwlaNBdrTcmm
0NkPohjxJlPbaAePDArzvlmunAnxhEgaiGYAxkTDx5bVapBIjM8kGZaj6njmwyGbyirwZfBO
v2DShPBpwdQKLP6XxJUFDkC/9gU4jQKcESxiBdKhPiqwposHkC3DShP78/FoKcLqC+AZEkC3
CpwZLL5P1znQV4TAAzhU4OIFOApYswDWj+QqZ68gU4TQKz9zFoKcHqC3cmFApwngU4TQKo4u
lHTK4joKc/zJnDpwHhU4uTaBUF+EqC3DVhCYGgDY69gU4GIF3znz9RV4zRV4zANSn3bGfJmT
O/aUFTEFgU4vHkCfcXHgqwdoKOhl1O1VueshqpUyCUF+IqCHRVMQK8RIFKnsIRoH4zQVAnP6
tgUsprLcDkyCrchbRV40ZmvBkCfEShPBb4hqwdoKcLizbBpwdQKcH4FgqwdoK8JUFnoHkibY
qxKp3AVx6lTQK8JIF+sjKvCVhPiqwZOhrgUm8bcz17iqwdn3zdnnzngUG9fEVh/Gnx78EASh
/uQKcPgL4MfuHwx0chQK+9Ymulo1WD4hqwnQfvCSxOxEqC3HVh7jqwdwInpJdCSh7AQMehBV
hvAVhb+6DLkCfCShbgImgr4zRV4+QI4nH5pb/Spxpe53tCfdz9NWXt14X2nsliT2ugBdACPj
WxOyPF/Zz20ppB1UwOajUBLnE6fG+Ce3TLKLxJlWtaUC6himxM1DDkUi5LQRxtshuHbxPdXd
q75mpPC7kIxYjiTQsXaenL6jiXf57+xL/I+xdXM9FzWjNY3IgjJ56BlYGkbEpXPiUfzAfmes
NHBipTiJTiZTi5TibRR7i4ZXe75kRp0RpsRp8RptWJ4DY/OTNZ7j4h6jVlG1kF6pL0zM6+WI
ndRO0Nqu1oi5rnGpj4Fo0koGiaucMbUKLweiMi3V1WpZXwIH8KMQgFp6Y1l1UCV/Sm3OI9L5
Tei5hx36h9FZVNNAoF672PRTflYMO9S19uQNIXkMFVRjYqej91Scq6X0j9UX1AuaClZElZTG
BVdJNyEVX8s3xWbEBiC9HN1hHbFD13RhBjJMNMLWkuMWsdWsYnfsAXtper2UvV7U9mocrn8u
pFgZ2pgJ9Gk4MckJuXN2HGVAEhpYN1sJa7bjpYpneiXDIhdMScsJTcNemZcRQjaXhW8kURoG
YJ2g9EhBM9YOLzE6M2Aje5LjexRzCfxxjHHrHgon/raDBQX8DkL8iZgR8U82UbZ+SVU4WI6B
cTPeg4g8BDeB0Uil+BQM1KqOBmyguASJjofgS6YzZW+2uM4tKuU5pErfBPTU7AfSA9peTBNh
5N5OK7sh8IrGWii7OPOIKrgnwQObXTDIrYr/bVN91yVQvvSpzVuxtZ9KVTXn+EVgDwPECI7T
7JEwKY/4LwcY4SMPa7uc4lwMtGnmabPJLfX+eX7Jb3ambi+x4t3kFDNY5ZmcL7EC5fn9dsQn
g0M81zfd83A/1lihzy2/fk8aoASRB3fxQj9PAR0K9jlSfasbhIJ9lvjcXvPwddg76A31BurD
cXH4uOwddg76A31BurDcXH4uOwddg76A31BurDcXH4uOwddg76/FcXHDvzuhNx4t72tLBUNd
Ajy2R0PTsTn+vhd6wPj6BZvUoxQthJ6ko9RwSf3+/XSGtZfKFLXH4jOwHdgP6Af0B+oD8RH4
jOwHdgP6Af0B+oD8RH4jOwHdgP6Af0B+oD8RH4jOwH93Gf0xx3MRI9+43hPaYU/MTId2cCpn
+tRfSMU++/t9A3GRMPngvW/bSz8XLHz9VvIrtg4r9R0NlbfjsILGg9BtXxicWy+k09ZpzYR+
f0pWyi8fuVWUNUYp9ly+12EAh8C1umDqeyv1al73WOKDYbstuOk1ynY0B8m/Qcglu/0qhm/7
vPy7aNuJyrMKPLer7XffU0bXflYeb25P0/1L04iizHp36YWtW4yOG+6KT/JdZHTUjYuZjvU3
pgl13y1d44mxdjHv71dsJ9duvD77RYuSk/DuvD37qXZeN9w9dEuvjw9dEuvjw9dEuvjw9dEu
vjw9dEuvjw9dEuvjw9dEuvjw9dEuvjw9dEuvjw9d8L477YkO68stRRbzv6veMxp5ZR55Jv1f
+Yiz3tNNfby3EP1/ToUvoZG=
}
The next two examples and base image are for fBm parameters. The
fBm parameters can simply change the coloring pattern and they can also distort
the trap shape. Try different values for the fBm Transfer function for the image
fBm2. The user should study the differences between the images fBm1 and fBm2.
 |
 |
| Base | fBm1 fBm scale = 30 |
 |
|
| fBm2 fBm weight = 0.1 fBm transfer weight = 1.0 fBm scale = 30 |
|
AttrfBmBase {
; Copyright © 2007 by Ronald Barnett.
::ckHFojn2tz1SPOOuR47DQ/fwwnSymxtElklnEoDmzeJBbukN3bwWi2Ww6VLye6uN2f8pqikS
U2djdXkEkFY5cYQV8RxiVVkfifwoPMKK1im/ydfa1KdtuRWsevWPeg3yFK56VvUXpPVsNNa1
JZ9xT6isY2qGxbyRVRKOpji2WRR8m88oF/jtqcUWVrVFr/n9dimqVcxYnUr/rJ3zyvnFFlv+
uPRWiW8Wp+UfVR7zN66BhStqUMor77KW/D4YWlseV/gosW/WRcUEM8xjy2+KZR/3kjgZu7Tt
ihh6ujk1Klda5Yxnj2sLPLNOilnyyuHUZRbjzSSx/LbVr4YXRS2m4kd5b/yKR3RY//5M2mk0
s87+0h+RwdEG3T8aNaRYtjWNIHLPJLPX0f4wqD1NyORLE4GlPu55DtrXBL+4bFr/7P3UL4i6
m+n1rRjM8gWq0FgbDiPa6gsIYyHGiR3NP7ewJv7T1dq6KpJtMK6UHg1urvTe3ng5M1VlEGGE
RymHUTdnUMuaUOIFaYKX7flNkrYdRMXDFA9j/rRxgaN4GQ0UhhdIjCayXh9qu4Npy6/wwegC
7ftpXBbGoty+m+RTj/NIEJwsG0cVtCqA0SwHGbFNm5DjiGeBzasvJGLqkHEQa30dR8qDPcoL
pQU2rgmMFgRbiNGoyMkhHUS01HogCFNh0B4mWz29cLNKRTDl2m2Aqz1DFY4ur/h+DPgdqIdU
6ow03gQDadkMat9vYq93PHE42m4WdqesYdbd3fY/fm/HXDbi2DP3VuvAyVdanKvQoFduYxQx
6/0afDIeUhpMK4pNm0snO8gdF66t+wbDy9F/4wYvWn89QDQp2opxRpoBTLt7L2uhtLJen1gq
SRjsUtHimR7MmpsFUZ4+EKwhMpiiDUKE6IG7o8U8+iPHnRiMQMhkSgutpkJTfiMdM1PO9Mnd
PVPswwYHoZj2kasBaYceoZj8t5pBymbx+ITajdgVP1Pcr3+EY1kUUwaxnALmdlj+UFZU0Ley
3Pf6ZR1CTiGqRQ7fjJaEgZZb+CJi+6mdkYKKm7vGNCrH1IMRcPPvRoXsMUCY48Fzef48Lgw9
GxYc5YpkMjCYJG7McGWe4CjtZkC4AfmBdSKZ7pTRDnxSOwCq6uJVwIQaGthrlklDIlGwkamp
Xvd2w5pI6wZavFb3XDnvNh0UHbSEN1Mnw7U70U76UNlbQT+DQZ9txK9ImTyycnHxyyYSaKnM
ZZ9IZwooEaAY1X0cqQPerLj5hNJZLSnXMu3F0Dmn9lad/tz/kE3ybyWUHLtV9SF1nXZsEuC7
mTHqBMzTC2wmag2bmOp6trLrVDuRqMCo5V1yr3iXNtjU8B3tHd7AciHBsU57EdUPhHJt3mCy
dLPwqey634JrEnTQ3TtcTatQSlpqHF6MHFBxLTNOdWYeFwp42FgiylypVKp62YZSFAONZRUu
rYe+g+F/Of3VkMQ80Y8ij2VFa8qFGhxSnv//QXmTBwl6MRdHoEtobIfQD3jTK3baA+GDArzv
lW4Te2PhEgaiWYAxkTDB69Kt0AkRGeWjMtR9+oZsspms4K8ivCXY7hpwnxU4OMlrv7XxJYFD
mC/jwU4TYKcETxCCdixngV4UU2DTh7hpwXAAcFsC3CrgTIlwU4WMFex118nG4zwK8ZEglYKc
HmCHwUMW4JrRfKxsceYK8ZMll+5VwKcHsC3cpFgpwnxU4zYKoY+13TK4TwKc/LKXipwnwU4u
raBYF+MsC3DWhCYGkDY59wU4GMF38z4+wK8lwK8FoGJL7NlfNoTG/WYFTEFwU4fEmCf6UHAr
wdwKOhrrdaqd9YDVzpkrgV4TwKcEWxgpwnwUocyVJC9IfBsC48RvHmiNddhbwUuyKX4WYFOd
p57gpwnwU4z4GewKcHsC3C58eYKcHmC3heBwKcHsCfGWxJ6hp4GmaqS6dgVse5MmCfGThv4q
ybgV4TwK8CnwNYKz+Ne46DhV4u775u7ztmChUm8fEVh/O3x78EASh/hQKcPkL4OfuHwx8ahQ
K+9YWurhrtGwDVhPD/eDkidhJUFuPqC3HVh7gROTL6MkC3BgY8CDqC/KUFu51HWIF+MkC3AR
MDXxXiqw9hQwnH5pbfp0MgziHqCvt5xW7LyIfyOrOKGRdAD4wUNk2OqPHfv54pz80mQrgTyG
pyiMSY4F4V7uttoqCXOaXqRJoHKKGXoeakkYmXeiibLG7fuDfsu6U/LtzP+6kgZsR5JImLNf
sF9C41X+uf6yPhPq7ipv4i1YD2DA4YY3OImZQuRkc7IS8ND8q8YbuBETmFZzipziZzibRR7m
4FX+6F2kUykU6kU2k0WrE8w1vzUL29MeZ+U1oRldleyV6pGdfLkVcRO2Ppu1oi5rvpdPr/Vo
kk4+hauaKbUJLxeiMiPU3VrLugRO4TXgALysxqLrpEq+1UvTO6Xzm9Ezkxv2p4ry6GaAQL07
1PRLftYKO9a9juQNIXymjqoRMVux+aMnq+V9UPN1tgryoMjoKd2IoqLpRmo+in9O2ZjIQUY4
opO8YnYs5BKMYMhphFxikrjFbXELy9jF4uNxb3m4tbnr3EVb9kzn3AmVnCm0XOirwxCxjqp+
woCgEMHrpmNRbfbMHL90ZeNgk0VQiTNZirxLMjLCaU7L1ivJVEaBWiNavRYETPm7wMhOjNwo
X21Rv4oFhv44prh1jQ0z/TshAoL+BylexMwIeKeHqh7zwPOVVW62I6R8QPed4o8JDOB0Ezy7
AImYFVnATZQVAJ2EqHokM1cqlntLje7iL1eKx6Xx7E1OQHGoP3bCoJMfB3RZvNkHZ1wSU805
xRRVNMDDls9ttgsqY9PW3O0IXB9+GlOX5G3m1rUt996TUBOA7QIfFx5bRDUDnHfFWDLBixsk
d552WzY2mj3uNhFBvXw0ecOzs2m+yzZ5fJz2HD+mXTHppb3ygvG20eS8W3asL+L72BpRLzz0
+w6hQBjzhc8SzQCJ+lzoN7jY0W1fQ3gga/ukT7fNMZ/B0Yb8rPiJ73jGb7DR/ZYyetTyUfQ8
lPzo98Dq/lTq9Ej22zo/aJ1eiRbz8DkaHI1OQqdgU7Ap2BStDkaHI1OQqdgU7Ap2BStDkaHI
1OQqdgU7Ap2BStDka/bXStTZso8dOioZRu2jT3GzyZs/HxEd8HxEdlY8ssLQD9/3oh+fAhxa
9zVyb/BV7z98uA3zBunDcPH4eOw9cg75A3zBunDcPH4eOw9cg75A3zBunDcPH4eOw9cg75A3
zBunfHunBFLLzRufA0Ttg/ipzZ4ne/fZen5iyzHJsgFUP/76/Iew+NyfEP+e47pEdlyf2/Ge
sL83wjAlzBKnDUOHocOQ5cgy5AlzBKnDUOHocOQ5cgy5AlzBKnDUOHocOQ5cgy5AlzElz5+U
On7+BPvNKLLem458/TIe+fjlp+4O
}